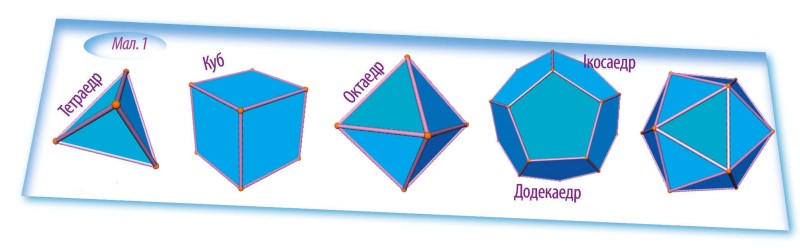
Ще у Стародавній Греції, понад два тисячоліття тому, люди знали про існування п’ятьох опуклих правильних многогранників. Правильними їх назвали тому, що їхні грані утворені однаковими правильними многокутниками, а вершини рівновіддалені від деякої точки, яку називають центром. Найменшу кількість граней має тетраедр, гранями якого є чотири рівносторонні трикутники. Далі йде куб із шістьма квадратними гранями. Октаедр має вісім трикутних граней, а дванадцять поєднаних між собою п’ятикутників називають додекаедром. Найбільше граней – двадцять рівносторонніх трикутників – має ікосаедр. Краї многокутників називають ребрами многогранника, а точки, у яких збігається кілька ребер, – його вершинами. Всі п’ять правильних многогранників ти можеш побачити на мал. 1.
Властивості многогранників вивчав видатний математик Леонард Ейлер. Він вивів формулу, що пов’язує кількість вершин (В), ребер (Р) та граней (Г) будь-якого опуклого многогранника:
В – Р + Г = 2
Також Ейлер довів теорему про те, що поверхню сфери можна покрити за допомогою дванадцяти правильних п’ятикутників та довільної кількості шестикутників.
Першим, хто надав особливого значення правильним многогранникам, був відомий давньогрецький філософ Платон – засновник філософської школи під назвою Академія. Тому правильні многогранники часто називають платоновими тілами.
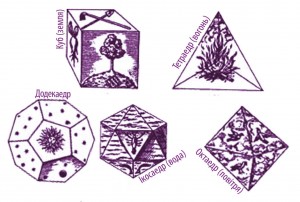
У своєму трактаті „Тімей”, написаному 360 року до н.е., Платон зіставив правильні многогранники з чотирма стихіями (землею, повітрям, водою й вогнем). Тетраедр уособлював вогонь, куб – землю, ікосаедр – воду, октаедр – повітря. Міркування Платона були простими і відповідали тогочасним уявленням про будову речовини: складені разом куби утворюють стійку, тверду, мов земля, систему. Вода, яка наче утворена із безлічі маленьких кульок (до них найбільш схожий ікосаедр), легко виливається з руки; гострі тетраедри жалять руку, неначе вогонь, а гладкі октаедри ковзають один відносно одного, і їх важко відчути, так само, як і повітря. Додекаедр займає особливе місце у Всесвіті і пов’язаний із п’ятою сутністю – ефіром. Божественна сутність додекаедра надихнула відомого іспанського художника Сальвадора Далі, і він використав його у своїй картині „Тайна Вечеря” (мал. 2).

Мал. 2
Довершеними формами правильних многогранників видатний німецький астроном Йоганн Кеплер намагався пояснити будову Сонячної системи. Цьому він присвятив свою роботу „Таємниці світобудови”, видану у 1596 році. На той час, окрім Землі, люди знали п’ять планет: Меркурій, Венеру, Марс, Юпітер і Сатурн. Кеплер розмістив орбіти цих планет у сферах, відстані між якими визначалися правильними многогранниками (мал. 3). Згодом йому довелося відмовитися від своєї ідеї, однак тривалі роздуми привели Кеплера до справді революційного відкриття – законів руху планет, що назавжди змінило розвиток фізики та астрономії.
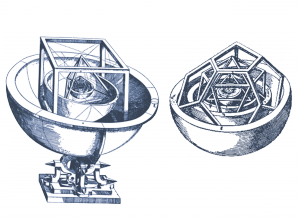
Мал. 3
Незвичайна архітектура
Учення про правильні многогранники збагатило не тільки філософію та астрономію. Геометричні ідеї знайшли своє втілення і в архітектурі. Визначний внесок у цю сферу зробив американець Річард Бакмінстер Фуллер.
Складне, проте плідне життя прожила ця людина, яка залишила по собі неабиякий спадок. Фуллер завжди керувався думкою: що потрібно зробити для тривалого й успішного виживання людей на нашій планеті. Він не мав систематичної освіти, вченого ступеня та власних коштів, але намагався з’ясувати, що такі особистості, як він, можуть зробити для поліпшення становища людства. Протягом свого життя Фуллер написав 28 книг, запровадив терміни, як-от „космічний корабель „Земля” і „синергетика”1. Він зробив величезну кількість винаходів, багато подорожував світом, виступаючи з лекціями, отримав чимало почесних учених ступенів та врешті досяг всесвітнього визнання. Найвідомішим його винаходом є так званий „геодезичний купол” – просторова сітчаста оболонка з прямих сталевих стрижнів, що нагадує сферу.
1Синергетика – теорія самоорганізації в системах різноманітної природи.


Мал. 4
Геодезичний купол має надзвичайну міцність та водночас порівняно невелику масу. Такими властивостями конструкція завдячує каркасній будові, утвореній рівносторонніми трикутниками (мал. 4). Навантаження рівномірно розподіляється по всіх елементах: що більша їхня кількість, то більшу вагу витримує купол. Зі збільшенням розміру купола об’єм простору під ним росте швидше, ніж об’єм самої металевої конструкції. Для підвищення міцності Фуллер використовував конструкцію із тетраедрів замість плоскої трикутної сітки. Його розрахунки показали, що для геодезичної сфери дуже великого радіуса маса каркасної оболонки товщиною понад кілометр буде нікчемно малою порівняно із масою повітря всередині сфери. Якщо це повітря нагріти всього лиш на один градус порівняно із довкіллям, то вся сфера ширятиме над землею без жодних двигунів, мов повітряна куля. На думку Фуллера, всередині таких сфер можна збудувати містечка із населенням у кілька тисяч осіб. Такі „дев’яті небеса”, як їх назвав Фуллер, могли б зависати на прив’язі або вільно перелітати з місця на місце (мал. 5).

Мал. 5
Втім, є ще одна річ, яка назавжди прославила ім’я Фуллера вже після його смерті.
Про сажу, діаманти, олівці та інше
Здавалося б, що може бути спільного між чорною сажею, що вкриває внутрішні стінки комина, та витонченими діамантами, які виблискують на світлі у коштовних оправах. А до чого тут ще й олівці? Усі ці несхожі між собою речі поєднує одне – хімічний склад речовин. Утворені вони лише одним хімічним елементом – Карбоном. У періодичній системі елементів він розташований під номером шість. Саме його використовують у хімії та атомній фізиці як еталон маси, адже 1/12 маси атома Карбону якраз і називається атомною одиницею маси. А чим ще цікавий Карбон?
Деякі хімічні елементи здатні до утворення двох або більше простих речовин. Такі речовини називають алотропними видозмінами або алотропами певного елемента. Незважаючи на однаковий хімічний склад, хімічні та фізичні властивості алотропів різні завдяки відмінностям у їхній будові. Оксиген, наприклад, може утворювати сполуку О2, що зветься киснем, або О3 – озон. Кисень потрібен для дихання всіх живих організмів, а озон захищає їх від згубного ультрафіолетового випромінювання Сонця. Та чи не найбільше алотропних видозмін має Карбон.
І сажа, і алмаз (діамант – це огранений алмаз), і графіт, що є серцевиною всіх простих олівців, є алотропами Карбону. Разючі відмінності у їхніх властивостях пояснюються різними способами поєднання атомів Карбону. В алмазі кожен атом Карбону утворює зв’язки із чотирма сусідніми атомами (мал. 6). У результаті отримуємо напрочуд міцну сітку (кристалічну ґратку), яка робить алмаз найтвердішим з усіх речовин. Графіт складається з багатьох плоских шарів із шестикутними комірками (мал. 6). Атоми Карбону у вершинах шестикутників закріплені доволі міцно, а от між сусідніми шарами взаємодія набагато слабша, тому вони легко ковзають одна відносно одної і можуть навіть відокремитися. Тому так зручно й легко писати олівцем.
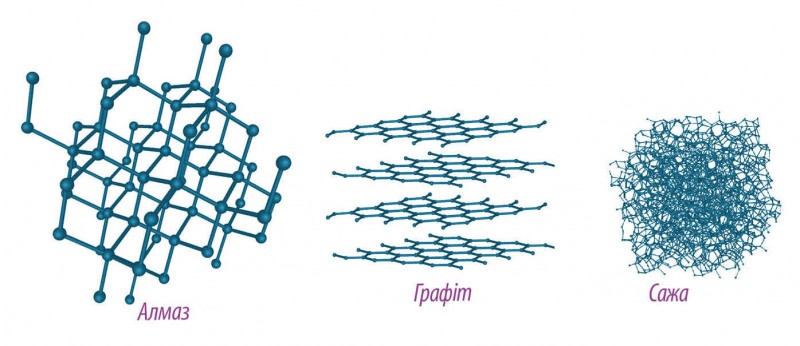
Мал. 6
Сажа, або ж аморфний вуглець, не має виразної структури, хоча насправді вона складається з величезної кількості мікроскопічних кристаликів (мал. 6). Сажу отримують штучно з різних сполук; серед частинок сажі подекуди трапляються доволі несподівані й цікаві об’єкти.
Фулерен та футбольний м’яч
Як це часто буває у науці, відкриття прийшло звідти, звідки його не чекали. Британський хімік Гарольд Крото займався вивченням міжзоряного пилу – дрібних твердих частинок, що заповнюють космічний простір та затьмарюють світло далеких зір. Його зацікавили частинки вуглецю, які входять до складу пилу. Щоб краще дослідити будову та механізм утворення цих частинок, Крото вирішив отримати такі сполуки в умовах лабораторії. Він звернувся по допомогу до своїх американських колег Роберта Керла і Річарда Смоллі, які досліджували випаровування графіту під дією лазерного випромінювання в Університеті Райса, що у Техасі, США.
Інтенсивні дослідження почалися 1-го вересня 1985 року і тривали десять днів. А вже 13-го вересня до престижного наукового журналу „Nature” учені надіслали статтю з описом результатів. Статтю опублікували у листопадовому номері цього журналу. В історію науки цей відтинок часу увійшов під назвою „десять вересневих днів” або „надзвичайна декада”.
У ході експериментів отримали незвичайні молекули, що складалися із шістдесяти атомів Карбону. Їхня форма нагадувала футбольний м’яч або вже відомі тобі геодезичні куполи Річарда Фуллера (мал. 7). На його честь Гарольд Крото запропонував назвати нову сполуку „бакмінстерфулереном” або просто „фулереном” – С60. Поряд із молекулами С60 вчені виявили також молекули С70. Відкриття молекули фулерену було визнане однією із найважливіших подій у науці XX століття, а Гарольд Крото, Річард Смоллі та Роберт Керл у 1996 році були удостоєні Нобелівської премії з хімії. У привітальному слові Нобелівського комітету це відкриття за значущістю прирівнювалося до відкриття Америки Колумбом.
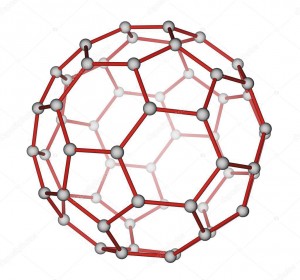
Мал. 7
Заради справедливості слід згадати, що теоретично можливість існування замкненої молекули з шістдесятьма атомами Карбону передбачив японський вчений Ейджі Осава ще у 1970 році. Щоправда, його стаття була написана японською мовою і тому не стала відомою широкому загалу. Трьома роками згодом радянські вчені Д. А. Бочвар та Е. Н. Гальперін детальними розрахунками показали, що повинна існувати стійка форма вуглецю, яка містить у молекулі 60 атомів Карбону. Але й ця стаття минула повз увагу наукової спільноти й на деякий час була забута.
Та повернімося до молекули фулерену. Якщо придивитися до структури молекули, стає помітно, що її каркас утворюють 12 п’ятикутників та 20 шестикутників. Точнісінько такий самий малюнок має поверхня сучасних футбольних м’ячів. Подивися на мал. 8 – схожість разюча! Кожен шестикутник межує з трьома шестикутниками й трьома п’ятикутниками, а всі п’ятикутники – лише з шестикутниками. Свого часу було сформульовано правило, яке назвали правилом ізольованих п’ятикутників. Суть його полягає у тому, що введення п’ятикутників у молекулярну структуру, утворену шестикутниками, викликає її хімічну нестабільність. Проте відомо, що молекула С₆₀ напрочуд стійка. Це пояснюється тим, що всі п’ятикутники каркасу молекули ізольовані.

Мал. 8
Згодом відкрили інші схожі молекули: С74, С84, С164, С192, С216… С540 (мал. 9). Молекула С70, наприклад, має ледь видовжену форму і схожа на м’яч для регбі. Каркас усіх фулеренів складається з 12 п’ятикутників та різної кількості шестикутників (згадайте формулу Ейлера). Проте саме молекула С60 є найбільш симетричною та округлою серед фулеренів. Найменша з відомих фулеренів – молекула С20, яка є додекаедром. Ця молекула дуже нестійка й отримати її важче, ніж інші фулерени.
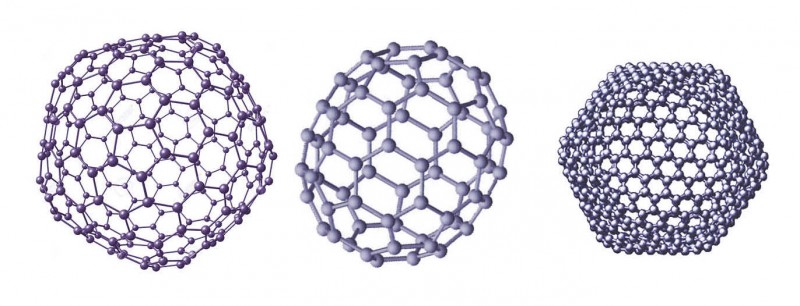
Мал. 9
Фулерен С60 – надзвичайна сполука. Його геометрична форма схожа до форми найважливіших білкових структур живих організмів. Фулереноподібну структуру мають віруси імунодефіциту, герпесу та поліомієліту, що відкриває можливість використання фулеренів для боротьби з цими захворюваннями. Фулерени привернули увагу науковців, які намагаються використати ці молекули для доставки ліків до пошкоджених органів людини.
У процесі життєдіяльності в організмі людини накопичуються так звані вільні радикали, які призводять до руйнування білкових структур організму. Особливо багато їх утворюється під час різних захворювань. Фулерени, завдяки своїм особливостям, здатні нейтралізувати вільні радикали. Всього лиш одна молекула фулерену може зруйнувати понад двадцять вільних радикалів.
На відміну від графіту й алмазу фулерен розчиняється в органічних розчинниках та утворює багато нових сполук із різними елементами. Вчені навіть примудрилися розмістити атом металу всередині молекули фулерену, неначе у клітці. На основі фулеренів виготовляють сухе мастило для зменшення тертя у механізмах. Кристали, утворені молекулами фулерену, по-різному пропускають світло різної інтенсивності. Такий ефект називають фотохромним. Його можна використати в оптиці або, наприклад, для виготовлення окулярів, що темнітимуть на яскравому сонячному світлі й ставатимуть прозорішими у приміщенні. Тривають дослідження щодо використання фулеренів у сонячних елементах та як резервуарів для накопичення та зберігання водню. Останнє має неабияке значення в енергетиці, а також для заміни бензинових двигунів електричними.
Це далеко не вичерпний перелік чудових властивостей та застосувань фулеренів. Роботи у цій галузі ще дуже багато, і хто знає, може, саме тобі випаде нагода зробити чергове відкриття у науці.
Що далі?
Карбон і надалі продовжує дивувати вчених. Так, були відкриті нові його алотропи – нанотрубки та графен. Вуглецева нанотрубка – це згорнута у циліндр сітка атомів Карбону, що розташовані у вершинах шестикутників. Діаметр трубок зазвичай становить приблизно 1 нанометр (одна мільярдна частка метра), а довжина може перевищувати його у мільйони разів. Кінці трубки можуть бути відкритими або ж заокругленими.
Графен – це плоска шестикутна сітка з атомів Карбону, своєрідна двовимірна гігантська молекула. Пригадай структуру графіту – якщо один шар атомів відокремити від решти, ми й отримаємо графен. Уперше це вдалося зробити вченим із Манчестерського університету у Великій Британії А. Гейму та К. Новосьолову у 2004 році. Вже у 2010 році за відкриття графену вони були нагороджені Нобелівською премією з фізики.
Просто диво, як несподівано переплітаються різні події, прояви природних явищ і наші ідеї та уявлення про них; якими невидимими зв’язками пронизаний увесь світ. Ми щойно побачили, що такі, здавалося б, різні речі, як філософія, архітектура, будова планетних систем та хімічних речовин, поєднані між собою доволі простими геометричними формами. А може, саме за простотою зовнішніх форм і ховається істина?
ЗАВАНТАЖИТИ СТАТТЮ У ФОРМАТІ PDF
























